Bài 1 trang 178 SGK Đại số và Giải tích 11
Bài 1. Cho hàm số
a) Chứng minh rằng: với mọi số nguyên
. Từ đó vẽ đồ thị
của hàm số
b) Viết phương trình tiếp tuyến của đồ thị tại điểm có hoành độ
c) Tìm tập xác định của hàm số
a) Ta có:
_ Từ kết quả trên ta suy ra hàm số là hàm số tuần hoàn có chu kì là
_ Do đó, ta chỉ cần vẽ đồ thị hàm số trên
và tịnh tiến nó song song với trục
các đoạn có độ dài là
Đồ thị hàm số :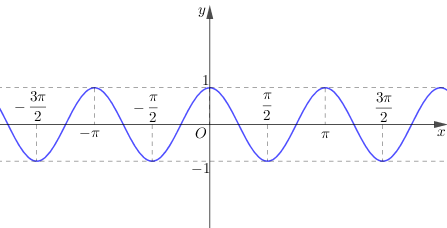
b) Ta có:
Ta lại có:
.
Vậy phương trình tiếp tuyến cần tìm là:
.
c) Ta có:
Mặt khác
Do đó, tập xác định của hàm số
Được tài trợ